Data Structures : Hash Tables Explained & Implemented in Java Part One
Sunday, August 29, 2021 Posted in Computer Science FundamentalsTags : Data-Structures Implementations Hash Tables
This is another post about Data Structures, about the Hash Table and it’s implementation in Java, we will look at Seperate Chaining based HTs in this post
Hash Tables are a very popular Data Structure implemented by default in many programming languages, it is the preferred data structure to store key-value pairs, and has a much faster “search” time for a “key” thanks to it’s design compared to others like Linked Lists and Arrays.
What is a Hash Table
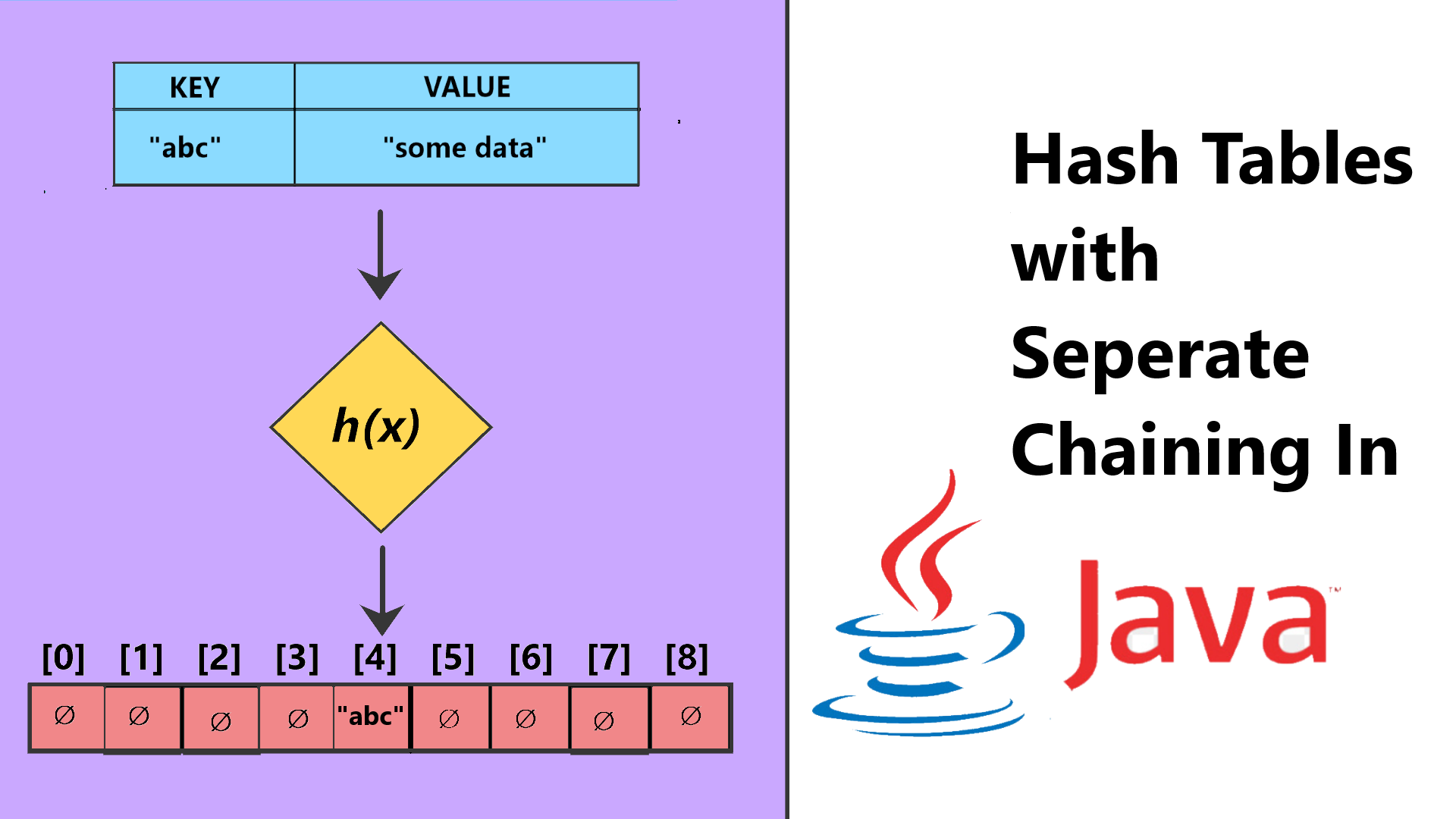
A Hash Table is an Array containing data which are key value pairs, this data is unordered since their Index in the Array is determined by the output of a hash function and a compression function upon the contents of the key of the key value pair, Searching for a particular key is easy since the key is first computed into it’s hash, and this hash is then checked with it’s corresponding index in the Hash Table array, making for faster look ups and retrieval.
Many times the Hash Function may output the exact same hash for different keys, leading to what is called a collision, to deal with this problem, there are two main types of collision resolution methods created for HT implementations, that is Seperate Chaining and Open-Addressing, we will be looking at Seperate Chaining in this post
Hash Table General Theory
As mentioned before, a Hash Table is simply an Array with key-value pair objects stored within it, that are indexed according to the output of a hash function on the key, the hash function in turn, is a function that performs some mathematical operations on the key, to output a number, this number may be very large, or may be a negative number, out of the bounds of our HT Array, for this purpose, we have a seperate compression function that “fits” our raw hash code into a number that will serve as an index in our HT array, this is done by removing the negative sign in the raw hash if any, and then modulo( % ) it by the size of the HT array, a modulo is simple getting the remainder of two numbers, for example a key “abc” may return a raw hash of 547 using the hash function h(k), we then pass this rawh hash code h into our compression function c(h) which is basically h % size, i.e assuming our HT Array has a size of 10, this will be 547 % 10 that is 7 which fits cleanly in our 10 slot sized HT array.
Too maintain good look up times on our HT, we have to periodically resize the underlying array, and rehash all the inserted key value pairs to new slots in the larger array, because of Academic research done on optimum values for HT, we now know that the optimum resize value for our HT array is 2 times the current size of the array, that is 2n where n is the size of the Array.
Another value we need to take care of is related to when exactly do we need to resize our array, this is determined using the threshold value, which is computed as loadfactor * size, now the load factor may be seen as a “percentage” of slots that are filled, and a good value is 0.75 for this, so again assuming our HT’s starting size is 10 elements, by computing the threshold as 0.75 * 10 and casting it to an int which gives us 7, i.e when 7 slots of our HT Array of size 10 are full, we resize it.
The above carries over even to the Linear Addressing paradigm, not just the Seperate Chaining method we implement in this post, to summarize,
- The new size is the current size doubled :
size =* 2 - The threshold value is :
t = loadfactor * size - loadfactor is set to
0.75by default and is an optimum value.
HT Seperate Chaining Theory
As mentioned before, Seperate Chaining and Open Addressing are the chief collision resolution techniques in HT implementation, SC does this by creating a container data structure called a Bucket which is mostly chosen to be a Linked List, to contain all the keys that have a colliding hash value, in essence you have the HT Array, and each slot can contain a Bucket( Linked List ) which contains the Key-Value pairs that share the same hash, a search function first produces the hash of the key that is being looked up, then checks the bucket that resides at that hash/index, for the same key, and then returns the key-value pair.
Open Addressing directly inserts the KVPs into the HT Array slots, there are no Buckets/Linked Lists involved, if there is a collision, that slot is skipped, there are 3 main paradigms to do this, but we will not be getting into Open Adressing techniques in this post
Seperate Chaining based Hash Table Implementation in Java
We will implement our HT in this section, for this we create two classes, Entry for the KVP object that will be inserted into our HT, and which will also contain our rawHash() method, and HashTable for the main logic of our code concerning the HT Array itself, the Buckets and the add(), find(), remove(), resizeTable(), printTable() methods.
Entry Class
Let’s get started with the Entry class, in the Constructor, we set the key and value properties using the parameters, and we also store the rawHash in this Entry object by running the rawHash(key) method, we do this so it is faster to just run the compression function on this Hash while resizing the HT Array, rather than running the rawHash function again for every existing KVP in the HT Array
class Entry {
public String key;
public String value;
public int rawHash;
public Entry(String key, String value) {
this.key = key;
this.value = value;
this.rawHash = rawHash(key);
}
public static int rawHash(String key) {
int hashKeyValue = 0;
for (int i = 0; i < key.length(); i++) {
int charCode = key.charAt(i) - 96;
hashKeyValue = hashKeyValue * 27 + charCode;
}
System.out.println("Key: "+key+" RAW HASH : "+hashKeyValue+"\n");
return hashKeyValue;
}
public String toString() {
return " { Key : "+this.key+" -> Value : "+this.value+" } ";
}
}
The rawHash function itself just runs some mathematical operations on each character of the given string, in order to produce a hash code, this hash code by itself will be either too large, or be a negative to fit in our HT Array as an Index, so we will run this rawHash through the compressionFunction we will see in the HashTable class.
Lastly for this class we define our own toString() method to pretty print the contents of the KVP, this function is automatically called when an Entry object is in a System.out.println() statement.
HashTable Class
The meat and potatoes of our HashTable file, where it all comes together, for the sake of brevity I am posting the class with just the constructor and properties first, later functions will be posted in snippets, So let’s get started
public class HashTable {
public LinkedList<Entry> bucket;
public LinkedList<Entry> hashTable[];
public int size, threshold, count = 0;
public double loadFactor = 0;
// load factor is a value using which we resize the hash table after a set number of
// elements are inserted, 0.75 chosen here will resize the table after it has reached
// 75% of it's capacity
final static double DEFAULT_LOADFACTOR = 0.75;
}
We will explain our properties now, we have a bucket variable of the type LinkedList<Entry>, what this means is it will be a Linked List taking in objects of type Entry, the next property is our HT Array that is hashTable[] this is also of the LinkedList<Entry> type since it will take objects of type LinkedList, i.e our Buckets.
Then we declare three ints size,threshold and count and initialize them to 0, size is the length of our HT Array i.e the max amount of elements it can contain, threshold is the value computer by loadfactor * size which will give us the “threshold” value of total elements inserted into the HT Array, after which it has to be resized, and count is the current amount of KVPs inserted into the HT array
Finally we get the default loadfactor as a constant LOAD_FACTOR to 0.75, However in the constructor up next this can be set to a custom value.
The Constructor
public HashTable(int size, double... loadFactor) {
hashTable = new LinkedList[size];
this.size = size;
if (loadFactor.length != 0) {
this.loadFactor = loadFactor[0];
// Threshold is load factor multiplied into size casted into an int
this.threshold = (int) this.loadFactor * size;
} else {
// Threshold is load factor multiplied into size casted into an int
this.threshold = (int) (DEFAULT_LOADFACTOR * size);
}
}
The constructor here takes in one compulsory parameter, that is size which is used to create the HT Array of the length size, and another vararg parameter that is a custom double loadfactor, but this can be left empty also, in which case the constructor will use the default value as shown by the if statement, the threshold value is then set to the int casted (int) output of the this.loadfactor * size statement.
Compression Function
public int compressionFunction(int rawHash) {
return Math.abs(rawHash) % size;
}
This is a simple function that takes the generated rawHash of an Entry object as a parameter, and returned the “compressed” version of it after removing the negative sign using Math.abs() and modulo( % ) it by the size of the HT Array, modulo is just the remainder operator, the standard divide / gives you the quotient, the result of this modulo operation will always be lesser that the size value, so as to fit as an index in the HT Array
Adding an Entry
public void add(String key, String value) {
Entry entry = new Entry(key, value);
System.out.println("CURRENT COUNT: " + count + " CURRENT THRESHOLD: " + threshold);
if (count > threshold) {
resizeTable();
}
int hashKey = compressionFunction(entry.rawHash);
LinkedList<Entry> bucket = this.hashTable[hashKey];
if (bucket == null) {
bucket = new LinkedList<Entry>();
}
bucket.add(entry);
this.hashTable[hashKey] = bucket;
count++;
}
This function takes two parameters of type String key and value, which are used to create an Entry object very creatively called entry, as we saw in the Entry class, a rawHash code is automatically generated while creating the object and assigned to rawHash property, so it can be accessed in the form entry.rawHash.
We then check if the current count of inserted elements is greater than the threshold in which case we resize the HT Array using resizeTable() the implementation of which we will see later, A hashKey is then generated by passing entry.rawHash to the compressionFunction which will then be used as an index in our HT Array
Then the bucket variable is set to the contents of this.hashTable[hashKey], since we do not initialize the slots of our HT Array to empty bucket objects in order to save space, empty slots will be null, so the next if statement checks for this, and creates a new LinkedList<Entry> and assigns it to bucket if it was null.
Lastly the entry is added to the bucket LinkedList using the bucket.add which is a function inbuild into the LinkedList collection, the bucket is set to this.hashTable[hashKey] i.e the slot of the index hashKey and the count variable is incremented.
Finding an Entry
public Entry find(String key) {
int keyHash = compressionFunction(Entry.rawHash(key));
LinkedList<Entry> bucket = this.hashTable[keyHash];
for ( Entry entry : bucket) {
if(entry.key == key) {
System.out.println("ENTRY FOUND { Key : '" + entry.key + "' -> Value : '"+entry.value+"' } AT INDEX [" + keyHash + "]\n");
return entry;
}
}
return null;
}
For this purpose the find() function takes the key as a parameter, and returns an Entry object if it is found, else null is returned, the keyHash is found by passing the output of Entry.rawHash(key) to the compressionFunction() as a parameter, rawHash is a static function, so it can be called directly from the Entry class without the need to instantiate an object by Entry.rawHash(key).
As in the previous function, we extract the bucket from it’s location in this.hashTable[keyHash], now since different Keys can hash to the same value, this means our buckets can have multiple Keys, so we use a for each loop to iterate through the Entry objects in the bucket, and compare the keys of the entry objects to the one specified in the parameter, if one if found, we print to the console with the details and index of the KVP, and return the entry object, else we return null.
Removing an Entry
public void remove(String key) {
int keyHash = compressionFunction(Entry.rawHash(key));
LinkedList<Entry> bucket = this.hashTable[keyHash];
for ( Entry entry : bucket) {
if(entry.key == key) {
// Remove entry from bucket
bucket.remove(entry);
System.out.println("ENTRY FOUND & REMOVED { Key : '" + entry.key + "' -> Value : '"+entry.value+"' } AT INDEX [" + keyHash + "]\n");
}
}
// If bucket is empty remove to save space
if(bucket.size() == 0) {
this.hashTable[keyHash] = null;
}
}
The code in this function is very similar to the previous one, but in the if statement of the foreach loop here, we instead use the bucket.remove(entry) function to delete our entry, this is a built-in function of the LinkedList collection, and we then print out data of the remove element, Lastly if the bucket in a slot is empty, we set it to null to save space.
Resizing the Hash Table
public void resizeTable() {
size *= 2;
threshold = (int) this.loadFactor * size;
System.out.println("DOUBLED SIZE : " + size);
LinkedList<Entry> newTable[] = new LinkedList[size];
for (int i = 0; i < hashTable.length; i++) {
if (hashTable[i] != null) {
for (Entry entry : hashTable[i]) {
// new Index for new table using old raw Hash stored in entry
int newIndex = compressionFunction(entry.rawHash);
LinkedList<Entry> bucket = newTable[newIndex];
if (bucket == null) {
bucket = new LinkedList<Entry>();
}
bucket.add(entry);
newTable[newIndex] = bucket;
}
}
}
hashTable = newTable;
}
In this complex function which is triggered when the inserted elements in our array cross the threshold value, we resize the Hash table, and repopulate it with rehashed KVPs from the current Hash Table, I will walk you through the function step by step.
The size is doubled firstly by size *= 2, so if the size was 10 initially after the resize, it will be 20, the treshold is also re-computed to make up for the newly doubled size, then a new HT Array is created called newTable[] of the newly doubled size.
A for loop is used to iterate through the current hashTable, and if the slot that is being currently iterated is not null, we get into a foreach loop to iterate throug the bucket in this slot, since it may get confusing, i’ve pasted this for each snippet below.
for (Entry entry : hashTable[i]) {
int newIndex = compressionFunction(entry.rawHash);
LinkedList<Entry> bucket = newTable[newIndex];
if (bucket == null) {
bucket = new LinkedList<Entry>();
}
bucket.add(entry);
newTable[newIndex] = bucket;
}
A newIndex i.e a hash code is created by passing the already existing rawHash value of the entry object to the compression function, we then set a bucket linked list to whatever is stored in newTable[newIndex], if this bucket is null, we create a new LinkedList, we do this step since this is a foreach loop, and the bucket in hashTable can have multiple entries, so if a new bucket is already created and inserted in one pass of the array, we don’t want to create new buckets and lost the data of the previous buckets, we then use bucket.add(entry) to push the entry objects into the bucket LinkedList, and then set the updated bucket to the newTable[newIndex]
Finally, we exit the main for loop and set the current hashTable field to the larger and updated newTable that we created in this function.
One More Thing
public void printTable() {
for(int i = 0; i <= hashTable.length-1; i++) {
System.out.println("Index ["+i+"] => "+hashTable[i]);
}
}
I’ve just created this short little function to pretty print our HT and it’s Buckets, works with the inbuilt toString of the LinkedList collection and the toString in our Entry class to create an ordered representation of our HT.
Putting It All Together
public static void main(String[] args) {
HashTable hashMap = new HashTable(10);
hashMap.add("abc","some text");
hashMap.add("def","some text");
hashMap.add("ghi","some text");
hashMap.add("jkl","some text");
hashMap.add("mno","some text");
hashMap.add("pqr","some text");
hashMap.add("stu","some text");
hashMap.add("vwx","some text");
hashMap.add("xyz","some text");
hashMap.printTable();
hashMap.find("xyz");
hashMap.remove("mno");
hashMap.printTable();
}
This is the main program to test out our HashTable and all it’s functions, around 8 KVPs are added to this HT of size 10, so as to hit the threshold that will be 7, and resize the table to one that is 20 elements long, we also test the find and remove functions and print the HT to verify their effects.
Conclusion
So that’s it for Hash Tables implemented with Seperate Chaining, hope you learnt a lot about this complex Data Structure and it’s Java implementation from scratch, perhaps I will make another post about HTs with Open Addressing techniques in the future, which is quite a broad topic in itself.
Full source code of the Hash Table with Seperate Chaining implemented here is on GitHub